
Each problem has them finding the area of a rectangle or a square. The students will be working with their tablemates on a roundtable. Tools: Practicing area with squares problems, square manipulatives Using the correct label falls under MP 6: using precision You can also ask them what happens when you multiply units by units? Students should see that you get u². Using squares also helps students make a connection with the label for area: u². Students should say they either counted all the squares or multiplied the side lengths together to get the area. I want students to find the area and explain how they got their solution. The last two problems have the rectangle and square on the grid. I will be using the squares for three of the five problems. Ask students if this matters when trying to find the area? Then ask them what property supports their answer? After students create the rectangle, ask them what the area of the rectangle is? In the power point, I’ve shown both ways the rectangle can be created.
This will help them when creating the rectangle for the first time using the squares. Ask students how many sides a rectangle has? What do they know about the side lengths of a rectangle. Remind students that when we find the area of a figure, we are finding how many squares will cover the whole figure. Students may struggle with creating the whole rectangle. By asking the students to transform the side lengths, create the rectangle, and find its area, we are using MP2. Students will represent the rectangle on their desk with the squares given.

We will get into specific units of measure when we use the formula.įor each problem, I’m asking the students to find out how many squares will cover a rectangle with certain side lengths. The size of the manipulative really doesn’t matter as I will be using units for each measurement. You can use the hundredths from the base 10 blocks or square pattern blocks. Each student or pair of students needs to have some square measuring tool.
#Rectangle area formula how to#
The formula states that \(A=l\times w\), so the area of the yard is \(30\text\).During this section, I will be having the students “act out” how to find the area of rectangles and squares. The length of the yard is 30 feet, and the width is 20 feet. This is a scenario where the area formula of a rectangle can be applied.

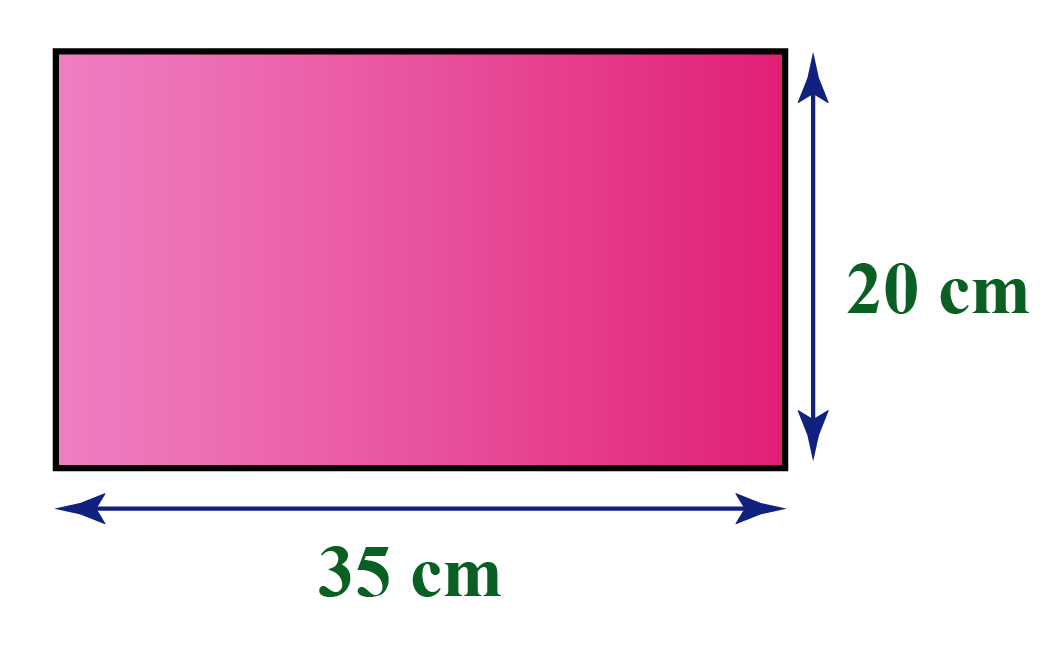
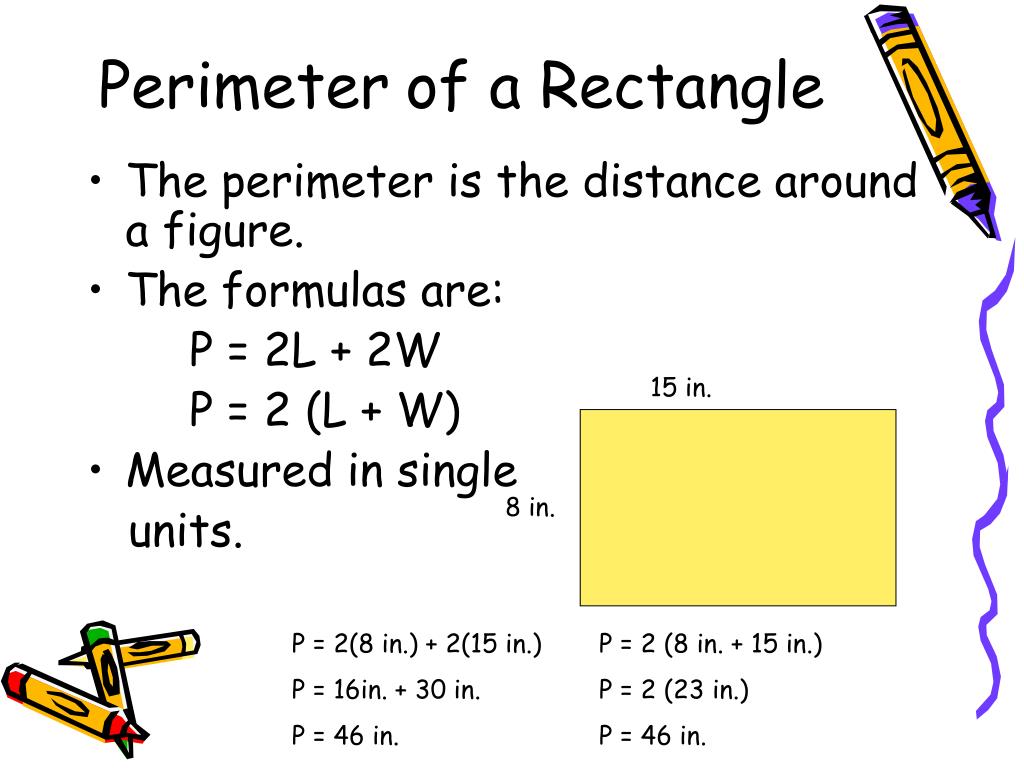
Do you have enough sod to cover the entire yard? Your yard has a length of 25 feet and a width of 30 feet. You want to determine if this is enough grass to cover the entire yard, so you need to compare the area of the sod to the area of your yard. You want to plant grass in your new backyard, and you currently have 645 square feet of sod available. In this case, our answer would be 640 m 2. Area is the result of multiplying two dimensions, length and width, which can be represented as a power of 2. The units associated with surface area will always be units squared. The area of the rectangle can be calculated by multiplying \(l\times w\), or \(32\times20\), which is 6,400. For example, the rectangle below has a length of 32 meters and a width of 20 meters. A represents area, l represents length, and w represents width. When determining the area of a rectangle, the formula \(A=l\times w\) can be applied. Situations such as these will require the use of surface area calculations. Area calculations are made for scenarios such as determining the number of tiles needed to cover the bottom of a swimming pool, the amount of wrapping paper needed to wrap a gift, or the amount of square footage you have in your backyard. Calculating surface area is a skill that can be applied in many real-world situations.


 0 kommentar(er)
0 kommentar(er)
